HashMap 精妙的设计细节

HashMap 可能已经被各大技术博文讲烂了, 在各种面试中也是频繁被问到; 本文不会再把前辈们的话复述一遍, 而是根据我的面试经历和一些使用心得, 总结一下 HashMap 源码中一些极少被注意到 (但仔细研究发现十分精妙) 的设计细节及使用注意事项;

首先统一申明两个概念:
HashMap 维护了一个数组类型的内部成员 table, 其中的每一个元素, 背后都是一个存放 hash 冲突的 KV 键值对的链表, jdk 的开发者将其称作 bin 或 bucket, 中文译作 “桶”, 故本文将统一使用 “桶” 作为相关概念的代称;
在 HashMap 中 KV 键值对信息被维护在一个继承自 Map.Entry 的内部封装结构中, jdk 的开发者将其称作 entry, 中文译作 “条目”, 由于中文含义容易引起歧义, 故本文将沿用 “entry” 作为相关概念的代称;

hash 逻辑的历史变革

HashMap 从 1998 年 jdk 1.2 诞生以来, 经历了多次重构, 愈加完善; 不过 jdk 1.6 之前的源码已经很难再找到 (只能在 github 上找到一些非官方的民间收藏版本, 想要准确对比 HashMap 在各个 jdk 版本中的实现差异已比较困难, 在网上仔细查阅各种资料文章, 竟发现在很多细节上互相冲突, 却也无从考证; 故本节将尽量总结设计思想方面的演进, 而尽量不陷入代码细节的纠结;

蛮荒时代

在 jdk 1.2/1.3 时代, HashMap 更多的是作为一种产品原型而存在, 关键的 hash 定位逻辑设计得比较简略:

只是简单的用 key.hashcode 作为一个 entry 的 hash 值, 对于 hash 冲突的避免能力不足;
取模逻辑使用的是高级运算符 %, 效率比较低, 当然与之对应的, 此时的 HashMap 还没有强制使用 2 的幂次方作为容量;
1
2
hash = key.hashCode();
index = (hash & 0x7FFFFFFF) % tab.length;

大刀阔斧改革

大神 Doug Lea 似乎对 jdk 原始的 hash 定位逻辑很不满意, 开始了大刀阔斧的重构, 从 jdk 1.4 开始, Doug Lea 成为了 HashMap 的第一作者;
首先是 hash 计算逻辑被单独抽出来治理, 从 jdk 1.4 到 jdk 1.7, 经历了两三次算法迭代; 这些算法的原理是类似的, 区别在于参数的调优, 算法主要是通过移位与异或运算, 以做到对 key.hashcode 充分打散, 组合其高位与低位的不同特征, 尽可能求出一个与其他 entry 不同的 hash 值;
jdk 1.4 的实现:

static int hash(Object x) {
    int h = x.hashCode();
    h += ~(h << 9);
    h ^=  (h >>> 14);
    h +=  (h << 4);
    h ^=  (h >>> 10);
    return h;
}

jdk 1.5 和 1.6 的实现:

final int hash(Object k) {
    h ^= k.hashCode();
    h ^= (h >>> 20) ^ (h >>> 12);
    return h ^ (h >>> 7) ^ (h >>> 4);
}

jdk 1.7 在 1.5/1.6 的基础之上增加了针对 String 类型的 key 的优化: sun.misc.Hashing.stringHash32 函数会以类似于 Murmur hash 的算法对传入的字符串快速算出一个 32 位 hash 值; Murmur hash 算法对于微小变化的输出扰动非常明显, 其已经在各种新型存储系统的散列功能领域里占领江湖, HashMap 借用该类库, 省时省力, 不用重复造轮子, 可谓再好不过;

final int hash(Object k) {
    int h = hashSeed;
    if (0 != h && k instanceof String) {
        return sun.misc.Hashing.stringHash32((String) k);
    }
    h ^= k.hashCode();
    h ^= (h >>> 20) ^ (h >>> 12);
    return h ^ (h >>> 7) ^ (h >>> 4);
}

除了 hash 函数的重点治理之外, Doug Lea 还针对 hash 值做取模运算确定下标的逻辑作了极致优化, 并专门抽出了一个方法:

1
2
3

static int indexFor(int h, int length) {
    return h & (length-1);
}

这个方法的设计非常巧妙, 它利用二进制的特性, 根据以下定理将比较高级的取模运算转化为了低级的逻辑与运算:

约定 $x \in N, n \in N$, 令 $c = 2^n$, 则有 $x \ \% \ c = x \ \& \ (c - 1)$

这个定理从二进制的角度上看, 理解起来很直观:

证:
约定 $bin(x)$ 的含义为 $x$ 的二进制表示;
$\because c = 2^n = 1 << n$ $\quad \therefore bin(c) = 1 \underbrace{00 … 0}_{n \ 个 \ 0}, bin(c-1) = \underbrace{11 … 1}_{n \ 个 \ 1}$;
情况 1: $0 < x < c$
此时 $x \ \% \ c = x$ 自不必说, 同时 $bin(x)$ 的位数 (去除前导 0) 必然小于等于 $n$ 位;
由于 $bin(c-1)$ 的 $n$ 位皆为 $1$, 根据逻辑与的特性, $x \ \& \ (c-1) = x = x \ \% \ c$

情况 2: $x \geq c$
设 $bin(x) = \underbrace{a_1a_2 … a_m}_{m \ 位}\underbrace{b_1b_2 … b_n}_{n \ 位}$, 其中 $m \geq 1$;
令 $x = a << n + b$, 其中 $a > 0$, $0 \leq b \leq c$;
则 $bin(a) = \underbrace{a_1a_2 … a_m}_{m \ 位}$, $\quad$ $bin(b) = \underbrace{b_1b_2 … b_n}_{n \ 位}$, $\quad$ $x \ \% \ c = b$
同理, 由于 $bin(c-1)$ 的 $n$ 位皆为 $1$, 根据逻辑与的特性, $x \ \& \ (c-1) = b = x \ \% \ c$

综上, $x \ \% \ c = x \ \& \ (c - 1)$

为了能够确保利用该定理给取模运算提效, Doug Lea 规定了 HashMap table 数组的 capacity 必须始终为 2 的幂次方, 并在各处加以卡控:

默认初始值是 16, 这个自不必多说;
后续扩容通过左移一位 (capacity << 1, 即乘以 2) 来实现;

如果在构造器中指定了 capacity, HashMap 会算出比给定值大的第一个 2 次幂作为实际的 capacity, 其计算方法如下所示:

static final int tableSizeFor(int cap) {
    int n = cap - 1;
    n |= n >>> 1;
    n |= n >>> 2;
    n |= n >>> 4;
    n |= n >>> 8;
    n |= n >>> 16;
    return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}

所以无论在什么情况下, capacity 一定是 2 的幂次方, 确保满足了定理中的条件, 这便是 indexFor 得以高效计算的前提;

趋于完善

jdk 1.7 在哈希散列这个事情上下足了功夫, 因为 jdk 的开发者想尽力避免 key 寻址冲突迫使 HashMap 退化为链表; 而在 jdk 1.8/1.9 里, 却突然走起了回头路: 只是简单得让 key.hashcode 的高 16 位与低 16 位做一下异或就草草了事了, 其他优化都省了!

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

我想这么做的原因是 jdk 1.8 优化了 key 寻址冲突排队入链的逻辑, 也就是下面小节将提到的 treeify (树化): 在一定条件下将链表进化为红黑树; 有了这样的优化, HashMap 查询时间复杂度退化为 O(n) 的问题解决了, jdk 的开发者便不再看重 hash 函数的冲突优化了, 所以就把 hash 函数的计算逻辑简化了, 这样能顺便提升一些性能;

final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
    Node<K,V>[] tab; Node<K,V> p; int n, i;
    if ((tab = table) == null || (n = tab.length) == 0)
        n = (tab = resize()).length;
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);
    ...
}

另外, jdk 1.8 不再单独拆出一个 indexFor 方法, 而是直接将这一精巧的取模算法内联到各个方法中了, 比如上面代码片段中的 tab[i = (n - 1) & hash], 降低了代码的可读性, 不过在非 JIT 优化的环境下可以减少一点调用开销;

扩容逻辑的优化

除了大名鼎鼎的 treeify 是 jdk 1.8 中人尽皆知的优化, 还有一处不引人注目的小优化其实也值得被提及: jdk 1.8 基于一个与 indexFor 方法使用的同宗同源的小定理, 优化了触发扩容时 entry 重新定位的逻辑;
先介绍一下该定理, 约定 $bin(x)$ 的含义为 $x$ 的二进制表示, $bin_idx(x, n)$ 的含义为 $x$ 的二进制表示中右起第 $n$ 位, 则可以引入如下定理:

若 $x \ \% \ 2^n = k$, 其中 $n \in N, x \in N$, 则有 $x \ \% \ 2^{n + 1} = \begin{cases} k & bin_idx(x, n + 1) = 0 \\ 2^n + k & bin_idx(x, n + 1) = 1 \end{cases}$

该定理其实是第一节中 $x \ \% \ 2^n = x \ \& \ (2^n - 1)$ 的衍生定理, 推演如下:

证: 由第一节的定理可知:
$x \ \% \ 2^n = x \ \& \ (2^n - 1) = k$
$x \ \% \ 2^{n+1} = x \ \& \ (2^{n+1} - 1)$
又知:
$bin(2^n-1) = \underbrace{11 … 1}_{n \ 个 \ 1}$, $\quad bin(2^{n+1}-1) = \underbrace{111 … 1}_{n + 1 \ 个 \ 1}$, $\quad bin(2^n) = \underbrace{1}_{第 n+1 位} \underbrace{00 … 0}_{n \ 个 \ 0}$

当 $bin_idx(x, n + 1) = 0$ 时:
$x \ \& \ (2^{n+1} - 1)$ 的 $n+1$ 位为 $0$, 而前 $n$ 位与 $x \ \& \ (2^n - 1)$ 相同, 则 $x \ \% \ 2^{n + 1} = 0 + k = k$;

当 $bin_idx(x, n + 1) = 1$ 时:
$x \ \& \ (2^{n+1} - 1)$ 的 $n+1$ 位为 $1$, 即第 $n+1$ 位的逻辑与计算结果左移 $n$ 位后为 $ 2^n$, 同时前 $n$ 位与 $x \ \& \ (2^n - 1)$ 相同, 逻辑与计算结果为 $k$, 则 $x \ \% \ 2^{n + 1} = 2^n + k$;

推演完毕;

定理中的表述已经清楚的反映了它在 HashMap 扩容重定位时的含义:

设 HashMap 的 capacity 为 $2^n$, 当发生扩容时, 第 $k$ 个桶内的 entry:
如果其 hash 的第 $n+1$ 位为 $0$, 则该 entry 还应放在第 $k$ 个桶里;
如果其 hash 的第 $n+1$ 位为 $1$, 则该 entry 应该放在扩容后的第 $2^n + k$ 个桶里;

对应的 jdk 1.8 源码如下:

// java.util.HashMap#resize
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
    next = e.next;
    // 通过 e.hash & oldCap 计算第 n + 1 位的值
    if ((e.hash & oldCap) == 0) { // 值为 0 放入第一条链
        if (loTail == null)
            loHead = e;
        else
            loTail.next = e;
        loTail = e;
    } else { // 值为 1 放入第二条链
        if (hiTail == null)
            hiHead = e;
        else
            hiTail.next = e;
        hiTail = e;
    }
} while ((e = next) != null);
if (loTail != null) {
    loTail.next = null;
    newTab[j] = loHead; // 第一条链放在原有的第 j 个桶里
}
if (hiTail != null) {
    hiTail.next = null;
    newTab[j + oldCap] = hiHead; // 第二条链放在扩容后的第 j + 2^n 个桶里
}

树化场景下的扩容

除了对于普通的冲突链表, 还要考虑到已经树化的桶, 扩容期间在拆分成两棵子树时, 也要保持逻辑一致, 使用上述定理执行优化; 按理说对一棵树做拆分, 实现上应该比链表要复杂一些, 不过 jdk 的作者做了一个小小的抽象复用, 把复杂性解决了:

// HashMap
static class Node<K,V> implements Map.Entry<K,V> {
    final int hash;
    final K key;
    V value;
    Node<K,V> next;
    ......
}

// LinkedHashMap
static class Entry<K,V> extends HashMap.Node<K,V> {
    Entry<K,V> before, after;
    ......
}

// HashMap
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
    TreeNode<K,V> parent;  // red-black tree links
    TreeNode<K,V> left;
    TreeNode<K,V> right;
    TreeNode<K,V> prev;    // needed to unlink next upon deletion
    boolean red;
}

jdk 的作者对 TreeNode 的注释里写到:

Entry for Tree bins. Extends LinkedHashMap.Entry (which in turn extends Node) so can be used as extension of either regular or linked node.

可以看到, jdk 1.8 之前的 HashMap.Entry 类被改名为 Node, 这么做主要是为树化后需要继承它的 TreeNode 做铺垫 (树结构中一般叫做节点, TreeEntry 的叫法不太合适), 这个 TreeNode 继承自 LinkedHashMap.Entry, 从而间接继承了 Node 类, 那么它便具有了像链表一样链接前后节点的功能, 同时这并不妨碍它作为一个树节点拥有左右孩子构建出红黑树, 所以 TreeNode 既是树, 也是链表, 这为扩容时使用上述定理优化提供了便利:

// TreeNode 拆分逻辑
// bit 为 old capacity
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
    TreeNode<K,V> b = this;
    TreeNode<K,V> loHead = null, loTail = null;
    TreeNode<K,V> hiHead = null, hiTail = null;
    int lc = 0, hc = 0;
    for (TreeNode<K,V> e = b, next; e != null; e = next) {
        next = (TreeNode<K,V>)e.next;
        e.next = null;
        // 通过 e.hash & bit 计算第 n + 1 位的值
        if ((e.hash & bit) == 0) { // 值为 0 放入第一条链
            if ((e.prev = loTail) == null)
                loHead = e;
            else
                loTail.next = e;
            loTail = e;
            ++lc; // 计算第一条链的长度
        }
        else { // 值为 1 放入第二条链
            if ((e.prev = hiTail) == null)
                hiHead = e;
            else
                hiTail.next = e;
            hiTail = e;
            ++hc; // 计算第二条链的长度
        }
    }
    if (loHead != null) { // 第一条链放在原有的第 j 个桶里
        if (lc <= UNTREEIFY_THRESHOLD)
            tab[index] = loHead.untreeify(map);
        else {
            tab[index] = loHead;
            // 若第二条链为空, 说明所有元素都在第一条链
            // 那么第一条链本身也是完整的树结构, 则不用重建红黑树
            // 只有第二条链不为空时, 节点被拆分了, 树结构不完整了, 才需要重建
            if (hiHead != null)
                loHead.treeify(tab);
        }
    }
    if (hiHead != null) { // 第二条链放在扩容后的第 j + 2^n 个桶里
        if (hc <= UNTREEIFY_THRESHOLD)
            tab[index + bit] = hiHead.untreeify(map);
        else {
            tab[index + bit] = hiHead;
            // 原理同上
            if (loHead != null)
                hiHead.treeify(tab);
        }
    }
}

总体而言, 相比于之前对每个元素都重新计算一遍下标值, jdk 1.8 改进后的算法在理论效率上还是有显著提升的, 不过由于在实际使用中, 冲突本就不会很严重, 同时我们为了避免扩容, 经验上会根据预估容量在初始化时确定一个合适的 capacity (比如 guava 的 Maps.newHashMapWithExpectedSize(int) 方法), 所以在实际生产环境里性能提升没有理论上那么显著, 但是这种顺手的优化也算是 “油多不坏菜” 吧!

并发修改触发 resize 的死循环

我们都知道 HashMap 是线程不安全的, 而且在以前我们总会被告诫: 如果对一个 HashMap 使用多线程并发操作, 轻则抛 ConcurrentModificationException 异常, 重则 cpu 打满, 请求无响应; 抛 ConcurrentModificationException 是 HashMap 对多线程操作的主动 check, 属于可控情况, 而 cpu 打满请求无响应则是某个桶内的冲突链表形成了死循环链, 程序已失控; 本节重点讨论一下 jdk 1.7 及之前版本死循环链的形成机制以及 jdk 1.8 对于此等情况的避免;
简化起见, 设定一个 HashMap 当前的 capacity 为 2, load_factor 为 1.0, 当前已有元素 a 和元素 b 被插入, 分布如下, 显然, 其已处于扩容前的临界状态:

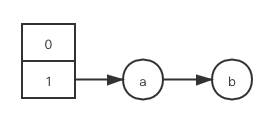
此时有两个线程 (thread1, thread2) 都想向其中插入新元素, 在插入之前首先它们需要面对的是 resize 方法; jdk 1.7 的 resize 方法中进而调用了一个关键的 transfer 方法:

void transfer(Entry[] newTable, boolean rehash) {
    int newCapacity = newTable.length;
    for (Entry<K,V> e : table) {
        while(null != e) {
            // 关键的一行代码
            Entry<K,V> next = e.next;
            if (rehash) {
                e.hash = null == e.key ? 0 : hash(e.key);
            }
            int i = indexFor(e.hash, newCapacity);
            e.next = newTable[i];
            newTable[i] = e;
            e = next;
        }
    }
}

注意到上方我注释的那行代码 Entry<K,V> next = e.next, 假设 thread1 执行完该行代码, 用完了自己的时间片, 线程对应的内核线程状态切换为 READY, 此时在 thread1 的本地工作内存里, 变量 e 被赋值为 a, 变量 next 被赋值为 b;
cpu 将计算资源调度给 thread2, 然后 thread2 很幸运, 在它的时间片内, 它执行完了 resize 方法的所有逻辑, 并将本地工作内存内的执行结果刷回主内存, 借用上一小节的说法, 我们设定 $bin_idx(a, n + 1) = bin_idx(b, n + 1) = 1$, 则此时 HashMap 的状态如下:

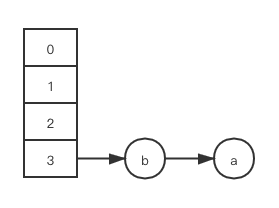
cpu 再次将计算资源调度给 thread1, 下面好戏开场了:
第一步: 从它被 cpu 切换前执行完的那行的下一行代码开始, 跑完 while 循环里剩余的逻辑, 此时在 thread1 的本地工作内存里, 变量 e 被赋值为 b, a.next 被赋值为 null, 此时 HashMap 状态如下:

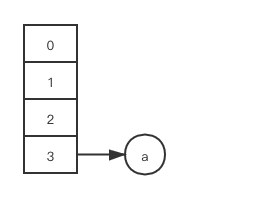
第二步: 假设此时 thread1 将主内存中的更新 (b.next 被赋值为 a) 及时刷回自己的本地工作内存, 又因为 e = b != null, 所以 while 循环再次被执行一轮, 此时在 thread1 的本地工作内存里, 变量 e 再次被赋值为 a, 此时 HashMap 状态如下:

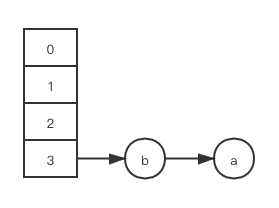
第三步: 因为 e = a != null, while 循环又会被执行一轮, 然而这是异常情况, 本不应该发生; 等跑完此轮 while 循环, 在 thread1 的本地工作内存里, a.next 被赋值为 b, 此时 HashMap 即出现死循环链:

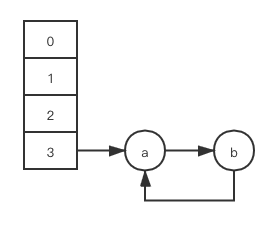
以上便是 jdk 1.7 及之前版本死循环链的形成过程, 我们可以发现, 死循环产生的根本原因是 jdk 1.7 采用头插法更新链表, 导致 resize 方法将冲突链表中的元素顺序作了倒置, 当某个线程抢先将链表转置的结果刷新至另一个滞后的线程本地工作内存时, 阴差阳错的事情就发生了!
所以 jdk 1.8 改成了尾插法, 当链表不再发生转置, 死循环链的情况自然便不复存在了; 当然这并不是说采用尾插法的 jdk 1.8 HashMap 就可以放心地使用多线程操作了:

ConcurrentModificationException 依然是避免不了的, 这是 HashMap 的主动检查;
采用尾插法后, 如果使用多线程操作, 虽不会造成死循环链, 但是链表节点指针错位仍会导致数据丢失;
treeify 的过程依然是线程不安全的, 多线程操作依然会导致 treeify 过程中的各种问题;

总之一句话: HashMap 没有加锁, 没有同步, 就不可能提供线程安全的环境, 它的定位就是线程不安全的, 无论在算法逻辑上怎么变化, 我们都不要抱以幻想;

负载因子的取值依据

负载因子 load_factor 是面试官经常问到的问题, jdk 的作者对这一参数的介绍略偏于定性:

As a general rule, the default load factor (0.75) offers a good tradeoff between time and space costs. Higher values decrease the space overhead but increase the lookup cost.

这只能勉强解释, 为什么不能取值太大或太小, 是因为时间代价与空间代价的权衡, 但是如果面试官锱铢必较, 非要作定量分析: 都是差不多的取值范围, 为什么默认的负载因子偏偏是 0.75, 而不是 0.70 或 0.80? 这就要求我们仔细推敲一下作者的取值依据了;
扩容是为了尽可能避免 hash 冲突, 虽然偶尔的 hash 冲突很正常, 但是无论如何, hash 冲突都是我们不期望发生的事情, 如果不及时扩容, 随着 entry 源源不断得被放入 HashMap, 总有一刻 hash 冲突发生的概率会大到我们无法接受的程度! 扩容, 便成了 hash 冲突概率大到一定程度后的必要措施;
这里有必要说明一下, 目前所说的 hash 冲突, 是指当一个桶里放入两个 entries 时就算, 至于一个桶里被放入三个甚至更多 entries 等更加严重的冲突, 我们就无需再考虑了; 为了便于求解当前的问题, 我将问题定义稍作转化:

假定一个 HashMap 当前的总容量为 $c$, 已经放入了 $n$ 个 entries, 求 $\frac n c$ 的最大值, 使得: 给定一个桶, 满足其当前没有任何 entry 的概率 $P(0) \geq \delta$ $(0 < \delta < 1)$, 其中 $\delta$ 是主观上认为能够尽量避免发生 hash 冲突的临界概率 (注: 桶内没有任何 entry 时, 将一个 entry 放入才不会冲突);

为何是求最大值? 因为在 $c$ 不变的情况下, $n$ 越大, 占有的桶越多, $P(0)$ 必然越小, $\frac n c$ 与 $P(0)$ 呈负相关变化, 给定了 $P(0)$ 的最小值, $\frac n c$ 必然有最大值, 而 $\frac n c$ 的最大值便是 HashMap 理想的负载因子 load_factor;
如何定量研究这个问题呢? 我们应当认定以下事实:

针对 HashMap 中一个指定的桶而言, 一个 entry 要么放入该桶内, 要么不放入该桶内, 不存在其他情况;
在正常情况下, 每一对 entry, 是否落在某个指定的桶内的概率是相同而互不影响 (独立) 的;
如果 HashMap 的总容量 capacity = $c$, 则一个 entry 落在某个给定桶内的概率为 $ p=\frac 1 c$;

其中事实 1 和事实 2 的描述表征了 “将 entry 放入 HashMap” 的过程满足 n重伯努利实验 的条件, 由此可以自然引出二项分布概率模型:

$P_k = C_n^k p^k (1-p)^{n-k} \quad (k \in N)$

我们尝试带入相关参数得到问题抽象:

已知 $\delta$ 为常数, 且 $0 < \delta < 1$, $c \in N$, $n \in N$, 求 $\frac n c$ 的最大值, 使得 $P(0)=C_n^0 (\frac 1c)^0 (1-\frac 1 c)^{n-0} \geq \delta$;

这看起来并非是一个可以轻松求解的问题, 需要使用一点等价替换的小技巧, 我花了点时间推导出来, 下面给出完整的求解过程:

解:
$P(0)=C_n^0 (\frac 1c)^0 (1-\frac 1 c)^{n-0}=(1-\frac 1 c)^n \geq \delta$
$\because n > 0, c \geq 16 \quad \therefore (1- \frac 1 c)^n > 0$
定义变量 $a$, 对不等式左右两边同时取 $a$ 的对数, 令 $a > 1$ 以满足单调递增的函数性质, 则有:
$log_a (1- \frac 1 c)^n \geq log_a \delta $
$\Rightarrow nlog_a \frac {c-1} c \geq log_a \delta$

$\because 0 < \frac {c-1} c < 1, \quad a > 1, \quad 0 < \delta < 1$
$\therefore log_a \frac {c-1} c < 0, \quad log_a \delta < 0$
$\therefore n \leq \frac {log_a \delta} {log_a \frac {c-1} c} \Rightarrow n \leq \frac {-log_a \frac 1 \delta} {log_a \frac {c-1} c} \Rightarrow n \leq \frac {log_a \frac 1 \delta} {log_a \frac c {c-1}}$

$\Rightarrow \frac n c \leq \frac {log_a \frac 1 \delta} {clog_a \frac c {c-1}}$

化简到此处看似已无法继续, 不过对其再稍作变形便可豁然开朗:

令 $k = \frac {log_a \frac 1 \delta} {clog_a \frac c {c-1}} = \frac {log_a \frac 1 \delta} {log_a (\frac {c-1+1} {c-1})^{c-1+1}} = \frac {log_a \frac 1 \delta} {log_a (1 + \frac 1 {c-1})^{c-1} + log_a (1 + \frac 1 {c-1})}$
令 $t = \frac 1 {c-1}$, 则有 $k = \frac {log_a \frac 1 \delta} {log_a (1 + t)^{\frac 1 t} + log_a (1 + t)} \quad (0 < t \leq \frac 1 {15})$
令 $a=e$, 此时满足 $a > 1$ 的条件, 则 $k = \frac {ln \frac 1 \delta} {ln (1 + t)^{\frac 1 t} + ln (1 + t)}$

到这里已经很明晰了, 表达式里出现了两个可以替换的等价无穷小:

当 $c \to \infty$ 时, $t \to 0$, 有:
$(1 + t)^{\frac 1 t} \sim e, \quad ln(1+t) \sim t$

则有 $lim_{t \to 0} \frac {ln \frac 1 \delta} {ln (1 + t)^{\frac 1 t} + ln (1 + t)} = lim_{t \to 0} \frac {ln \frac 1 \delta} {ln e + t} = ln \frac 1 \delta$
即: $\frac n c \leq k \to ln \frac 1 \delta$

综上, $\frac n c$ 的最大值为 $ln \frac 1 \delta$

至此我们求得了 load_factor 关于 “冲突临界概率 $\delta$” 的函数, 我们便可以从量化的角度重新审视一下 HashMap 负载因子的取值依据了; $\delta$ 既然被定义为 “主观上认为能够尽量避免发生 hash 冲突的临界概率”, 那么这个概率取多少比较合适呢?
从感性的角度看, 如果一个事件发生的概率大于 50%, 我们便倾向于事件会发生, 反之则不认为; 那么 50% 的 hash 冲突概率可以作为 $\delta$ 的参考; 取 $\delta = 0.5$, 则 load_factor = $ln \frac 1 \delta = ln 2 \approx 0.693$, 好像比 HashMap 默认的 0.75 小了一点;
如果根据 HashMap 默认的 0.75 反过来推 $\delta$ 呢? $ ln \frac 1 \delta = 0.75 \quad \Rightarrow \frac 1 \delta = e^{0.75} \approx 2.117 \quad \Rightarrow \delta \approx 0.472$, 确实比 0.5 小了一点点, 不过在付出了 3% 的概率损耗之后, 却收获了如下好处:

load_factor 的选择要在时间代价与空间代价之间做权衡, 0.75 相比 0.69 显然有更优的空间复杂度, 尤其在有大量 entries 被放入的场景下;
在第一节中介绍了 HashMap 的 capacity 必须要满足 2 的幂次方, load_factor 取 0.75 可以保证算出来的 threshold 是整数, 不会因为四舍五入造成不必要的偏差;

这或许便是 jdk 开发者倾向于使用 0.75 作为默认负载因子的考量, 当然第二个理由有点勉强, 因为我查阅了 HashMap 的历史版本, 早在 1998 年 jdk 1.2 第一版 HashMap 诞生时, load_factor 就已经被默认赋为 0.75 了, 而那时默认的 capacity 是 101 (一个诡异的数字);
面试官对于这样的回答是不是可以不用再追问了?

treeify 的一些细节

在第一小节已经提到了 jdk 1.8 里, 在一定条件下, HashMap 会将因为寻址冲突而构造的链表转化为红黑树; 那么这个条件 HashMap 是如何界定的呢? 我们可以看到在 HashMap 的源码中定义了几个阈值:

1
2
3

static final int TREEIFY_THRESHOLD = 8;
static final int UNTREEIFY_THRESHOLD = 6;
static final int MIN_TREEIFY_CAPACITY = 64;

MIN_TREEIFY_CAPACITY 定义了触发转化红黑树的最小总容量是 64;
TREEIFY_THRESHOLD 定义了针对某个桶, 触发转化为红黑树的冲突链表长度为 8;

HashMap 中定义了如下方法以支持转化:

1	final void treeifyBin(Node<K,V>[] tab, int hash);

该方法主要在 putVal, compute/computeIfAbsent, merge 等涉及插入 KV 的方法中, 在判断条件满足之后被执行;
关于上面提及的三个阈值, 也有一个细节值得讨论: 第一个 TREEIFY_THRESHOLD 被设置为 8, 是经过了严谨的数学计算得出来的:
我们可以从 jdk 的开发者角度去想: 我们为什么要树化一个链表? 因为其对应的桶里元素冲突太大, 严重影响了 HashMap 的查询性能; 冲突本是在所难免的, 偶尔冲突也很正常, 针对这种正常的冲突, 我们没有必要对其做树化; 我们真正要树化的是那些异常情况, 比如因为 key 不合理导致的大量 hash 冲突, 甚至是有人恶意发起的哈希冲突攻击; 我们现在要给定一个阈值, 用以区分正常情况和异常情况, 冲突量小于阈值时暂且判定其属于正常, 不做树化, 只有当冲突量大于等于阈值时才触发树化; 这个阈值要满足, 正常的情况下, 冲突数量达到这个阈值的可能性几乎为 0, 以避免错判而产生不必要的树化开销;
在第一节的讨论中我们已经知道, “将 entry 放入 HashMap” 的过程是服从二项分布的, 但是在一个 HashMap 的生命周期中, 放入其中的 entry 数量 $n$ 是不确定的; 在第一节中, 我们只关心 “目标事件发生 0 次的概率” 这一特殊的场景, 从而简化了参数带入, 并且我们当时的目标并非求得具体的数值, 而是推算 $\frac n c$ 的比值, 此值与 $n$ 的具体值无关, 因此我们成功套用了二项分布的公式求得了最终结果; 但本小节的场景已完全不一样, 不可能继续套用;
不过好在, 当 entry 放入的数量足够多时, 我们可以进一步将 二项分布 转化为 泊松分布 (通常当实验次数 $n \geq 20$ 且目标事件发生概率 $p \leq 0.05$ 时, 可以用泊松分布近似二项分布), 而这正是我们寻找合理阈值的关键模型:

$P_k = \frac{\lambda^k}{k!} e^{−\lambda} \quad (k \in N)$

将以上泊松分布的概率分布公式对应到我们具体的问题中去, 其中 $k$ 表示有 $k$ 个 entries 发生 hash 冲突被放入同一个桶中, $P_k$ 表示发生这种冲突的概率; $\lambda$ 是数学期望, 表示一个桶平均有多少个 KV entry ; 由此我们的问题可以抽象为:

已知 $\lambda \geq 0$, 求 $k$ 的值, 使得 $P_k = \frac{\lambda^k}{k!} e^{−\lambda}\approx 0$;

要求解 $k$, 我们须先获得数学期望 $\lambda$; 不过这并非一件容易的事情, 泊松分布是二项分布的近似, 尽管我们知道二项分布的数学期望 $E(x)=\sum _{k=1}^{n}k{p_k}=\sum _{k=1}^{n} k C_n^k p^k(1-p)^{n-k}=np$, 但是这个公式无法直接套用到泊松分布里, 因为泊松分布的 $n$ 是不确定的, 正因此大学概率统计课本上关于泊松分布的题目, 大多是 “根据经验观察” 直接给定一个 $\lambda$, 然后求其他的问题; 不过, 我们可以换个思路, 既然泊松分布的 $n$ 是一个变量 ($n \in N$), 我们不妨根据 HashMap 的特性先建立一个关于 $n$ 的数学期望函数 $f(n)$:
我们手上有三个条件, (1) 第一节所述, 事实 3 中描述的事件发生概率 $p=\frac 1 c$; (2) HashMap 默认的初始容量 $c=16$; (3) HashMap 默认的负载因子 load_factor = $0.75$;
当 $0 \leq n \leq 12$ 时, $c=16$, $p = \frac 1 {16}$, $\lambda = np=\frac 1 {16}n$;
当 $n>12$ 时, 开始触发扩容, 当 $n$ 增加到 $0.75c$ 时, 立即触发 c *= 2, 由此可做如下归纳:

n 的取值范围	c 的值	补充说明
$\big[0,12\big]$	$16$	不适用于最后一行的归纳
$\big(12,24\big]$	$32$	/
$\big(24,48\big]$	$64$	/
$\big(48,96\big]$	$128$	/
…	…	/
$\big(12 \cdot 2^t,24 \cdot 2^t \big]$	$2^{t+5}$	$t \in N$

令 $n=12 \cdot 2^t+i \quad (0 \leq i < 12 \cdot 2^t)$, 则 $p=\frac 1 {2^{t+5}}, \lambda=np=\frac {12 \cdot 2^t+i}{2^{t+5}}=\frac 3 8 + \frac i {32 \cdot 2^t}$
于是我们可以建立函数:

$f(n)=\begin{cases} \frac 1 {16}n & 0 \leq n \leq 12 \\ \frac 3 8 + \frac i {32 \cdot 2^t} & t \in N, 0 \leq i < 12 \cdot 2^t (n>12) \end{cases}$

我们应当注意, 该函数的建立与 HashMap 的负载因子 load_factor 存在密切联系, 如果有使用者自定义了 load_factor, 函数的参数会发生显著变化; 不过极少有情况需要我们去定制 load_factor, 在上一小节我们已经证明了 HashMap 默认的负载因子 0.75 是一个比较合理科学的值, 本着简化问题的目的, 我们暂且将 load_factor = 0.75 作为固定系数;
$0 \leq n \leq 12$ 时的图像:

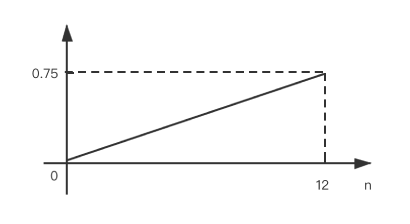
显然, $f(n)$ 在定义域上是线性递增的, 且 $0 \leq f(n) \leq \frac 3 4$;
$n>12$ 时将 $n$ 由 $i$ 带入的图像:

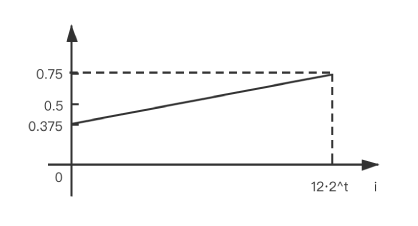
依托 HashMap 的特性, 我们发现 $n > 12$ 的情况下, 给定参数 $t$, $f(i)$ 在定义域上是线性递增的; 若将 $t$ 拓展到整个定义域, 可以绘制出完整的图像:

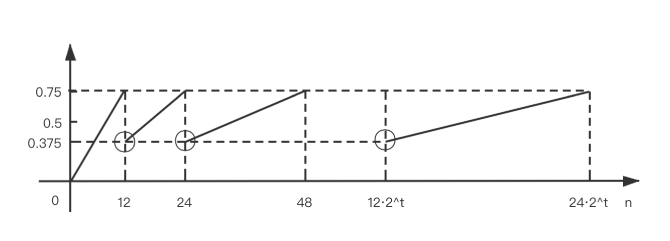
在参数 $t$ 的每一个取值所对应的 $n$ 的取值范围上, $f(n)$ 都分别呈现出线性递增的特性, 且 $\frac 3 8 < f(n) \leq \frac 3 4$;
至此, 关于实验次数 $n$ 的数学期望函数 $f(n)$ 的基本特征已经明晰了; 试验次数 $n$ 是随机而不可预测的, 也不存在一个可以估计的概率, 一种可能的处理方法是取平均值: 当 $0 \leq n \leq 12$ 时, $\overline{\lambda}=\frac {0+\frac 3 4}2=0.375$; 当 $n>12$ 时, $\overline{\lambda}=\frac {\frac 3 8 + \frac 3 4}2=0.5625$; 当然, 在不追求精确的场景下, 完全可以取一个范数来代表, 比如 jdk 在 HashMap 的类注释里就说明了, 在默认 load_factor = 0.75 的条件下, 他们将指定泊松分布的数学期望参数 $\lambda$ 设定为了 $0.5$:

Ideally, under random hashCodes, the frequency of nodes in bins follows a Poisson distribution with a parameter of about 0.5 on average for the default resizing threshold of 0.75, although with a large variance because of resizing granularity.

带入 $\lambda=0.5$ 至上述方程中: $\frac{0.5^k}{k!} e^{−0.5}\approx 0$, 这时就可以求解 $k$ 了, 于是 jdk 在类注释中列举了不同 $k$ 值对应的概率 $P_k$:

0: 0.60653066
1: 0.30326533
2: 0.07581633
3: 0.01263606
4: 0.00157952
5: 0.00015795
6: 0.00001316
7: 0.00000094
8: 0.00000006
more: less than 1 in ten million

由以上计算结果可知, 当 $k=8$ 时, $P_k \approx 0$, 即正常情况下一个桶内的 hash 冲突数达到 8 的概率几乎为 0, 一旦达到, 即可判定此为异常情况, 应当触发树化逻辑; 至此, 我们终于找到了 TREEIFY_THRESHOLD 被设置为 8 的由来;
除此之外, 还有两个与 treeify 相关的参数:
MIN_TREEIFY_CAPACITY 是触发树化的 entry 总数阈值, 当被放入的 entry 数量小于此值时, 只做扩容缓解冲突, 不做树化, entry 数量达到此值才会真正触发树化 (能用钱解决的就不用拳头, 最后没办法了再死磕);
UNTREEIFY_THRESHOLD 是触发由红黑树退化回链表的桶内 entry 数量阈值, 被设定为 6 而不是更接近于 TREEIFY_THRESHOLD 的 7, 是为了防止发生反复, 导致在链表与红黑树之间来回频繁转化消耗计算资源;

HashMap 实现: jdk 1.8 vs 1.7

根据经验, 面试官尤其喜欢问一些关于 HashMap 的实现对比, 比如 jdk 1.7 和 1.8 之间的实现差异等等, 其实很多已经在上面的篇幅中提及了, 我再作一个总结:

jdk 1.7 的 hash 方法对 key.hashcode 做了充分的四次异或运算, 而 jdk 1.8 则只做了一次 (具体见 hash 逻辑的历史变革);
扩容时, jdk 1.7 会遍历整条冲突链表对每个 entry 重新计算定位, jdk 1.8 则是根据 entry hash 值二进制表示中的右起第 n + 1 位拆成两条链, n + 1 位为 0 则放入原所在桶不变, n + 1 为 1 则放入新桶, 新桶的下标为原所在桶下标 + 扩容前的 capacity (具体见扩容逻辑的优化);
jdk 1.8 中新写了一个 Node 类代替原本的 Entry 类, 其意在打通整个 HashMap 家族对元素的包装, 是 LinkedHashMap.Entry 与 HashMap.TreeNode 的基类 (具体见扩容逻辑的优化);
当发生 hash 冲突时, jdk 1.7 会在链表的头部插入, 而 jdk 1.8 会在链表的尾部插入 (具体见并发修改触发 resize 的死循环);
在 jdk 1.8 中, 如果 entry 的总数达到 64, 且某个桶的冲突链表长度增长到 8, 链表将转换为红黑树; 反之, 当某个桶的冲突链表长度减少到 6, 红黑树将退化为链表 (具体见treeify 的一些细节);
jdk 1.7 插入新元素时, 会先检查是否需要扩容 (有必要则扩容), 然后再插入新元素, 而 jdk 1.8 则是反过来的; 关于此调整, jdk 作者并未解释原因, 我只能稍加揣测:
如果插入一个 entry 之后会触发 resize, 那么先做 resize 再插入该 entry, 是不是可以减少一点对该 entry 重新定位的计算量? 这或许是 jdk 1.7 及之前版本的优化考量;
其实插入新元素, 在检查是否需要扩容之前, 还有一步必须执行的逻辑: HashMap 必须先检测该 entry 是否已经存在, 如果存在则替换 value 后直接返回, 这涉及到对冲突链表的遍历; 对于采用尾插法的 jdk 1.8, 检测元素存在性的遍历是一个完全可以复用的逻辑, 如果不复用, 想要把元素插入到链表末尾就得付出额外的代价:
(1) 以时间换空间, resize 之后再遍历一遍, 插入末尾;
(2) 以空间换时间, 额外维护一个指向链表末端元素的指针, 以方便快速插入, 同时还要维护一个记录链表长度的变量, 以判断是否达到树化条件 (jdk 1.8 在复用链表遍历逻辑的同时, 顺手实时计算了链表的长度, 这些额外的空间开销都可以省了);
由此可见, 不复用遍历逻辑的代价是比较昂贵的, 不复用唯一能带来的好处, 也就是减少对新插入元素重新定位的计算量, 也在 jdk 1.8 的按位分类优化中得到改善, 开销并不明显; 从而, 选择复用遍历逻辑, 先于 resize 方法插入元素, 就成了 jdk 1.8 的最优选择;
反观 jdk 1.7, 由于是采用头插法, 本身复杂度就是 O(1), 不存在 jdk 1.8 的问题, 采用后于 resize 方法插入元素, 也在情理之中了;

HashMap 精妙的设计细节

2019-11-21
jdk

HashMap 精妙的设计细节

hash 逻辑的历史变革

蛮荒时代

大刀阔斧改革

趋于完善

扩容逻辑的优化

树化场景下的扩容

并发修改触发 resize 的死循环

负载因子的取值依据

treeify 的一些细节

HashMap 实现: jdk 1.8 vs 1.7

参考链接

HashMap 精妙的设计细节

hash 逻辑的历史变革

蛮荒时代

大刀阔斧改革

趋于完善

扩容逻辑的优化

树化场景下的扩容

并发修改触发 resize 的死循环

负载因子的取值依据

treeify 的一些细节

HashMap 实现: jdk 1.8 vs 1.7

参考链接

感谢支持!